魔方的原理是什么?(魔方的原理是什么,有什么技巧解开魔方)

一,魔方的原理是什么?
首先要知道魔方是由厄尔诺·鲁比克在1974年发明的,又以鲁比克来命名魔方,叫鲁比克魔方(英文名Rubik's Cube)。魔方的所有变化数量43,252,003,274,489,856,000种。如果你一秒可以转3下魔方,不计重复,你也需要转4542亿年,才可以转出魔方所有的变化,这个数字是目前估算宇宙年龄的大约30倍(魔方只有26个块)。而每个形态对应的公式,公式后又出现的形态,真的是千变万化。三阶魔方基本有无数种还原方法。而事实上上帝之数20步就能还原魔方。

魔方有6种色6个面,国际定色:白色为底公式D,黄色为顶公式U,蓝色在前公式F,绿色在后公式B,橙色在左公式L,红色在右公式R。魔方又分为6个中心块(每面最中间的块),8个角块和12个棱块组成。中心块是固定的结构,靠转动角块和棱块复原魔方。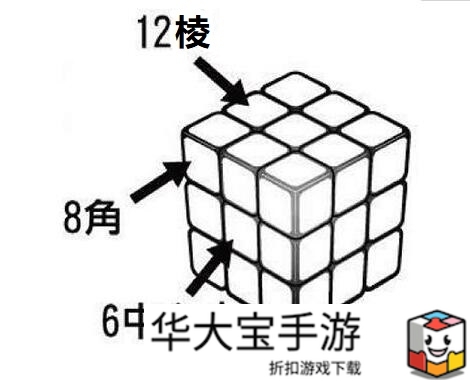
魔方还原的解法有很多种,常用的有层先法、高级玩法、棱先法、角先法和桥式解法等等。
1、层先法思:①先做好底部十字,②底层角块归位,③第二层棱块归位,④做顶成十字,⑤还原顶成颜色,⑥顶层棱块归位,⑦顶层角块归位。完成复原!
2、高级玩法:①做好底部十家,②还原前两层,③还原顶层颜色,④顶层角块、棱块一次归位。完成复原!
3、棱先法思路:①底棱归位(等同层先法十字),②边棱归位,③转八角。完成复原!
4、桥式解法思路:①做好左右桥,②顶角还原,③调整颜色朝向,④6棱归位。完成复原!
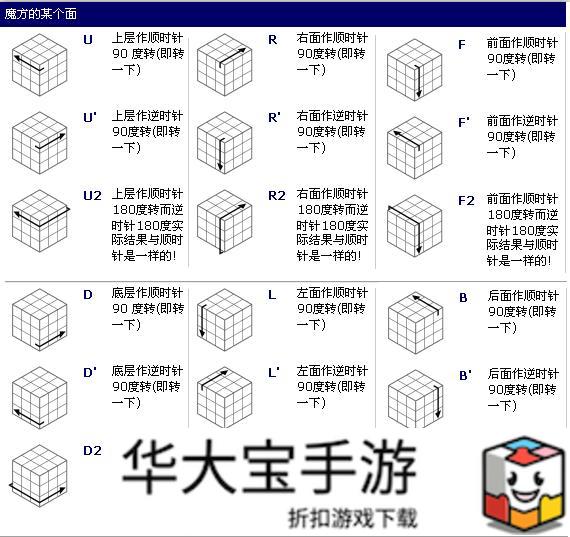
魔方转动记号
不管转动任何一个面,有2就转动两下,没有就转一下。如果没有带“丶”记号的就是正转,可了理解为顺时针转动或者拧紧瓶盖,拧紧螺丝等。带“丶”记号的则反之。
二,魔方的原理是什么视频
(小石头,站在偏数学的角度,来回答这个问题。简单一句话,魔方的原理就是:魔方群在状态集上的作用,具体回答如下:)
魔方群
整体来看,魔方(Rubik's cube)是一个立方体,一共有六个面 (surface),我们分别用 U(up 上)、D(down 下)、F (front 前)、B(back 后)、L(left 左)、R(right 右)来标识,不妨规定:U 对应 黄(yellow)、D 对应 白(white)、F 对应 蓝(blue)、B 对应 绿(green)、L 对应 橙(orange)、R 对应 红(red)。
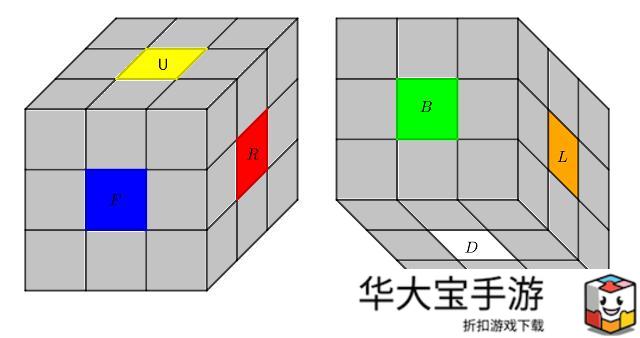
令,M = {U, D, F, B, L, R},当 任意面 f ∈ M 朝向我们时,对 f 面 顺时针 旋转 90°, 被定义为 魔方的 基本操作(base operation),同样用 f 面 的 面标识 来表示 这种基本操作。所以 M 也代表 魔方的全部基本操作。
对于,任意 基本操作 g, h ∈ M,gh 称为 g 和 h 的 复合(compose), 表示 先 g 操作 再 h 操作 的复合操作。可以验证,复合满足结合律, 这样以来,以 M 为生成元 在复合操作下会生成一个群 G = (M),称为 魔方群(Rubik‘s cube group)。其中,G 的 幺元,记为 1, 表示 没有进行任何操作的操作。
什么是群?
群就是定义了一种运算 的集合 ,其 满足:
集合对运算封闭,即,对于任意 都有 ( 注意:和乘法运算类似,习惯省略不写 ) ;
运算有分配律,即, 对于任意 都有 ;
有幺元,即,存在 使得 对于 任意 都有 ;
有逆元,即,对于任意 都存在 的逆元 使得 。
什么是 M 生成的群?
数学上定义:包括 M 中元素的 最小的群,为M生成的群,记为 (M)。实际上,可以 对 M 中任意操作 g 和 h 不断的 进行 复合运算,如果得到的新复合操作 gh 不在 M 中,就 gh 添加到 M 里,直到 M 不再增加,这样就得到了 (M)。
同一基本操作 g, 连续四次 复合 就是 对 g 面 顺时针 旋转 360°,这相当于 没有操作,即,
gggg = 1
从而有:
gg³ = 1
也就是说 g³ 就是 g 的逆元 g⁻¹ ,相当于 对 g 面 逆时针 旋转 90°。
另外,由 gggg = 1 还可以得到:
g²g² = 1
这说明 连续两次 复合 g² 的逆元 就是自己,即,顺时针 旋转 180° 相当于 逆时针 旋转 180° 。
魔方状态
三阶魔方被细分为 3 × 3 × 3 = 27 个 立方小块(cubie)。其中,位于 中间核心的 那个 小块 不会受到 魔方操作 的影响到,而对于 每个 面中心的 那个 小块 魔方操作 同样无法改变它的位置,因此 魔方操作 所能 影响到的 小块 为 27 - (1 + 6) = 20 个。
这 20 个 受 魔方操作 作用的 小块,又分为 两类:
位于魔方 8 个角 处的 角(corner)块,它们有3个有效 小面(facet);
位于魔方 12 个棱 处的 棱(edge)块,它们有2个有效 小面;
由于,每个面的 中心块 保持位置不变,因此对于打乱的魔方,可以依照 中心块 来 确定 魔方的各个面 方向。魔方在初始(或 还原)状态下,角块 和 棱块 的每个 小面 和 该小面 所在面 的 中心小块 颜色保持一致。
我们用 角块(或 棱块) 的各小面 颜色所对应的 标识 的小写字母 的组合来标识 角块(或 棱块):
对于 角块,三个小面 x, y, z,有 6 种排列方式,这里 使用 从 u 或 d 开始 的 顺时针 排列方式,即,角块标识 xyz 保证 x = u/d 并且 x →y → z 是顺时针;
对于 棱块,二个小面 x, y, 有 2 种 排列方式,这里 使用 从 u 或 d(f 或 b) 开始 的 排列方式,即,棱块标识 xy 保证 x = u/d/f/b;
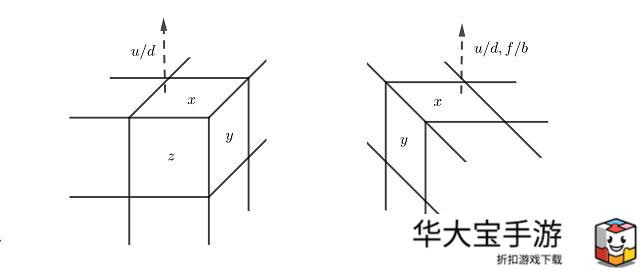
根据上面的规则,八个角块分别表示为:ufl, urf, ubr, ulb; dbl, dlf, dfr, drb; 十二个棱块分别表示为:ub, ur, uf, ul; bl, br, fr, fl; db, dr, df, dl
注意:六个中心块 分别表示为:u, d, f, b, l, r,核心块 一般用 o 表示 。
更进一步,对于角块 xyz,我们用 xyz 表示 x 小面,yzx 表示 y 小面,zxy 表示 z 小面,对于棱块 xy ,我们用 xy 表示 x 小面,用 yx 表示 y 小面,于是,我们就得到了 带有标注 的 8 × 3 + 12 × 2 = 48 个 小面。将,全体小面记为 T,则 任意 操作 g ∈ G 就变成了 T 上的 一种 置换(位置变换)。以 F 操作 为例,

观察发现, 小面 fur 经过 F 操作 置换 为 小面 flu,即,F(fur) = flu,另有 F(flu) = fdl、F(fdl) = frd、F(frd) = flu,于是 在 F 操作下,以上 4 个置换 形成了 一个 置换圈:

我们称其为 轮换(cycle),记为 (fur flu fdl frd) 。
参与轮换的 小面 可以是任意多个,值得注意的是:任何一个小面 a 的 轮换 (a) 相当于 不做 置换,有, 1 = () = (a) 。
当然,实际上 F 操作 包含 多个 轮换,将这些轮换 以复合的方式,聚合在一起,就是定义了一个 完整 F 操作:
F = (fur flu fdl frd) (fu fl fd fr)(rfu ufl lfd dfr)(rf uf lf df)(rdf urf luf dlf)
同理,我们可以将 其它魔方操作 定义为 轮换 的复合。
注意:为了方便,我们也可以用 1- 48 的 正整数,来替代 上面 S 中 对小面 的编码。
T 上的所有 置换函数,在函数复合下,组成 置换群 S₄₈。但是,因为 角块的面永远置换不到棱块的面,所以 G 仅仅是 S₄₈ 的子群。
用离散的小面来记录魔方的状态过于粗犷,重新审视魔方,我们会得到如下结果:
每个立方块都是一个整体,在任何魔方的操作下,组成它的小面不会分离;
每个立方块,有两种状态信息:位置 和 方向;
角块 和 棱块 在 魔法操作下 相互独立,即,角块 永远不可能 转到 棱块 上,反之亦然。
基于,以上分析,我们首先, 分别 对 角块 和 棱块 进行定位(location):
角块:ufl = 1, urf = 2, ubr = 3, ulb = 4; dbl = 5, dlf = 6, dfr = 7, drb = 8;
棱块:ub = 1, ur = 2, uf = 3, ul = 4; bl = 5, br = 6, fr = 7, fl = 8; db = 9, dr = 10, df = 11, dl = 12;

令 C = {1, 2, 3, 4, 5, 6, 7, 8}, 这里包含 所有 角块的位置信息,可以很容易将 基本操作 对 角块位置的 改变写成轮换形式:
U = (1 2 3 4),
D = (5 8 7 6),
F = (1 6 7 2),
B = (3 8 5 4),
L = (1 4 5 6),
R = (2 7 8 3)
显然,G 作用在 C 上 是 置换群 S₈ 的子群。
同理,令 E = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12},基本操作对于 棱块 位置的改变写成轮换形式为:
U = (1 4 3 2),
D = (9 10 11 12),
F = (3 8 11 7),
B = (1 6 9 5),
L = (4 5 12 8),
R = (2 7 10 6)
同样,G 作用在 E 上 是 置换群 S₁₂ 的子群。
然后,我们分别对 角块 和 棱块 进行定向(orientation):
角块:u/d 为定向面,xyz = 012;
棱块:u/d/f/b 为定向面,xy = 01;

对于保持 定向 信息,我们只需要定义,定位位置 当前 立方块 的 定向面 对应 的 编号就可以了。而对于 基本操作,对 定向的 改变,我们也只需要 记录,原始状态下,经过 基本操作后,各个 定位位置,的 定向面 对应 的 编号就可以了。如果,原始状态下,即, 定向面的编号为 0,经过某操作,到新位置后,定向面编号为 n,则 原来 定向面的编号为 m,经同样操作,到新位置后,定向面编号就是 (n + m) mod k,对于角块 k = 3,对于 棱块 k = 2。0- 不旋转,1-逆时针旋转,2-顺时针旋转。
令,V = (0, 0, 0, 0, 0, 0, 0, 0) 表示 角块的所有定向,则 基本操作为对角块定向的改变为:
U = (0, 0, 0, 0, 0, 0, 0, 0),
D = (0, 0, 0, 0, 0, 0, 0, 0),
F = (1, 2, 0, 0, 0, 2, 1, 0),
B = (0, 0, 1, 2, 1, 0, 0, 2),
L = (2, 0, 0, 1, 2, 1, 0, 0),
R = (0, 1, 2, 0, 0, 0, 2, 1)
对于每一位来说都是 Z₃ ,总共 8 个 Z₃ 就是 Z₃⁸ ,但是 考虑 在 到 7 个 角块固定的情况下,我们无法 单独 旋转 剩下的那个,因此 G 在 V 上的作用 实际上 是 Z₃⁷。
令,W = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) 表示 棱块的所有定向,则 基本操作为对棱块定向的改变为:
U = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0),
D = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0),
F = (0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0),
B = (1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0),
L = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0),
R = (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
同理, G 在 W 上的作用 是 Z₂¹¹。
当以上编号混合在一起使用时,为了区分,分别用 c、e、v、w 作为 角块定位、棱块定位、角块定向、棱块定向 编号的前缀,并将编号写成下标。例如:
F = (c₁ c₆ c₇ c₂) (e₃ e₈ e₁₁ e₇) (v₁, v₂, v₀, v₀, v₀, v₂, v₁, v₀) (w₀, w₀, w₁, w₀, w₀, w₀, w₁, w₁, w₀, w₀, w₁, w₀)
辅助工具
在进行下一步分析之前,我们先编写一点 JavaScript 代码,以帮助我们,对 G 中的 操作进行复合。
魔方状态(state)的 格式为:
state:[[角块定位], [棱块定位], [角块定向], 棱块定向]
声明 魔方初始状态 s₀ 如下:

魔方操作(operation)的 格式为:
[[[角块轮换], ...], [[棱块轮换], ...], [角块旋转], [棱块旋转]]
基本操作声明如下:

声明,在给定状态上执行魔方操作的函数:

声明,从给定状态中分析出魔方操作的函数:

定义 复合 函数:

为了输出简洁,当所有角块(或,棱块)不发生旋转 时,用一对空括号表示。
最后,我们对基本操作进行必要的扩展:

换位子 和 共轭
对于 任意两个 魔方操作 g,h ∈ G,如果,g 和 h 的复合 满足交换律,则:
gh = hg
等式两边右乘 g⁻¹h⁻¹,有:
ghg⁻¹h⁻¹ = hgg⁻¹h⁻¹ = h1h⁻¹ = hh⁻¹ = 1
如果 不满足交换律,则:
ghg⁻¹h⁻¹ ≠ 1
令,[g, h] = ghg⁻¹h⁻¹,称其为 换位子(commutator)。
一般来说,魔方相对面 ,如: F 和 B,U 和 D,L 和 R 之间是可以交换的,即,
[F, B] = [U, D] = [L, R] = 1
所有,换位子 之间是可以交换的,即:
[[g₁, h₁] [g₂, h₂]] = 1
关于,换位子有 性质1:如果 g 和 h 两种操作,只 共同影响 一个 小块 k,其中 g 为 n → k,h 为 m → k,则有 [g, h] = (k, n, m),[h, g] = (k, m, n)。
例如,若 g = (c₁ c₂ c₃), h = (c₁, c₄ c₅),则 k = c₁, n = c₂, m = c₄,于是有:

即,[g, h] = (c₁ c₂ c₄),[h, g] = (c₁ c₄ c₂)。
性质1推论:如果 g 和 h 两种操作,共同影响 的小块,刚好 在 g 和 h 中 分别 形成 轮换 σ 和 τ,则有 [g, h] = [σ, τ]。
例如:若 g = (c₁ c₂ c₃ c₄)(c₅ c₆), h = (c₁ c₂ c₄ c₃)(c₇ c₈),则 它们的共同影响小块 c₁、c₂、c₃、c₄,分别 在 g 和 h 中,组成轮转 (c₁ c₂ c₃ c₄) 和 (c₁ c₂ c₄ c₃),于是有:

即,[g, h] = [(c₁ c₂ c₃ c₄), (c₁ c₂ c₄ c₃)]。
魔方群中还有另外一种 称为 共轭(conjugate)的复合方式:对于 任何操作 g,h ∈ G,称 ghg⁻¹ 为 h 关于 g 的共轭。
共轭具有 性质2:如果 h = (a b c) 而 g 将 A, B, C 分别映射到 a, b, c,则有 ghg⁻¹ = (A B C)。
例如:若 h = (c₁ c₂ c₃), g = (c₁ c₄)(c₂ c₅)(c₃ c₆),则有:

即,ghg⁻¹ = (c₄ c₅ c₆)。
魔方公式
好了!现在利用上面的知识,就可以开始构造魔方公式了。
寻找角块的换位公式
我们发现 B⁻¹ 关于 R⁻¹ 的 共轭 R⁻¹B⁻¹(R⁻¹)⁻¹ = R⁻¹B⁻¹R:

和 F²:

仅有 c₇ 共同影响,于是它们满足 性质1,有:

即,[R⁻¹B⁻¹R, F²] = R⁻¹B⁻¹R F² (R⁻¹B⁻¹R)⁻¹ (F²)⁻¹ = R⁻¹B⁻¹R F² R⁻¹B⁻¹R F² = (c1, c7, c8)。
注意:因为 (ab)(b⁻¹a⁻¹) = abb⁻¹a⁻¹ = a1a⁻¹ = aa⁻¹ = 1,所以 (ab)⁻¹ = b⁻¹a⁻¹。
这里 c₁, c₇, c₈ 不共面,考虑 R² :

刚好 将 1 ↦ 1, 2 ↦ 8, 3 ↦ 7,于是根据 性质2,有:

开头的 RR RRR = R ,于是最终得到 公式C:

即,
R²[R⁻¹B⁻¹R, F²]R⁻² = RB⁻¹RF²R⁻¹BRF²R² = (c₁ c₂ c₃)
寻找棱块的换位公式
我们定义一种新的操作 M:面对 F 面,顺指针旋转 F 和 B 面之间那个中间的面M。M 操作 只改变棱块:

我们发现 M⁻¹(或 M)与 U²:

共同影响 e₄,因此 根据性质1,[M⁻¹, U²] 构成三轮换:

即,[M⁻¹, U²] = M⁻¹U²MU² = (e₂ e₄ e₁₀)。
其实,M⁻¹ 就相当于 FB⁻¹ 的复合,只不过,在执行 M⁻¹ 后,还做了 R 面朝向了 U 的动作。

这时 执行 U² 相当于 执行 R²,于是翻译为 基本操作 [M⁻¹, U²] = FB⁻¹R²BF⁻¹U²,验证:

最后, 根据 性质2,利用 R²U 将 这个 三轮换,换到同一个面上:

倒数第2, 3 项合并后,就得到了 公式D:
R²U[M⁻¹, U²]U⁻¹R² = R²UFB⁻¹R²BF⁻¹UR² = (e₁ e₃ e₂)
寻找角块的旋转公式
观察 D² 关于 RF⁻¹ 的共轭 RF⁻¹D²FR⁻¹:
 与 U²:
与 U²:

它们,有共同的轮转 (c₁ c₃),于是根据 性质1推论,有:
[U², RF⁻¹D²FR⁻¹] = [(c₁ c₃), (c₁ c₃)] = (c₁ c₃)(c₁ c₃)(c₃ c₁)(c₃ c₁) = (c₁ c₃)1(c₃ c₁) = (c₁ c₃)(c₃ c₁) = 1
这样以来,[U², RF⁻¹D²FR⁻¹] 就没有了位置变换,仅仅剩下的就是旋转:

于是,我们就得到 公式 E:
[U², RF⁻¹D²FR⁻¹] = U²RF⁻¹D²FR⁻¹U²RF⁻¹D²FR⁻¹ = (v₁, v₀, v₂, v₀, v₀, v₀, v₀, v₀);
公式 E 分别 对 c₁ 和 c₃ 进行 逆时针 和 顺时针 旋转。
寻找棱块的旋转公式
M 和 U 分别执行4次会恢复,那么 MU 执行四次,即,(MU)⁴ 是什么呢?

我们神奇的发现:
(MU)⁴ = F⁻¹BLF⁻¹BDF⁻¹BRF⁻¹BU = (w₁, w₁, w₀, w₀, w₀, w₀, w₀, w₀, w₀, w₁, w₀, w₁)
即,(MU)⁴ 只对 e₁, e₂, e₁0, e₁₂ 旋转;
同样,(MU⁻¹)⁴ :

(MU⁻¹)⁴ = F⁻¹BL⁻¹F⁻¹BD⁻¹F⁻¹BR⁻¹F⁻¹BU⁻¹ = (w₀, w₁, w₁, w₀, w₀, w₀, w₀, w₀, w₁, w₀, w₁)
即,(MU⁻¹)⁴ 只对 e₂, e3, e₁0, e₁₂ 旋转;
因为 棱块旋转 2 次就等于没有旋转,于是 (MU)⁴ 和 (MU⁻¹)⁴ 的复合 结果 只对 e₁ 和 e₃ 进行旋转,这就是 公式F:
(MU)⁴(MU⁻¹)⁴ = (w₁,w₀, w₁, w₀, w₀, w₀, w₀, w₀, w₀, w₀, w₀)
可以验证:

暴力搜索
两轮换 称为 对换,在魔方群中 单独的 对换操作,是不可能的 因此 三轮换,成立 公式构造的 关键,除了上面利用 性质1 来 找寻 三轮换 的 方法为,我们还可以用计算机,进行暴力搜索。例如:在 2 个 R,3 个 R⁻¹, 3 个 U, 2 个 U⁻¹ 的全排列中,进行三轮换搜索:

我们得到:

即,R⁻¹U⁻¹RURURU⁻¹R⁻¹U⁻¹ = (e₃ e₄ e₁₀)。然后 根据 性质2,利用 R² 将 这个 三轮换,换到同一个面上:

同样,将开头的 5 个 R 合并,就得到 和 公式D 类似的公式:
RU⁻¹RURURU⁻¹R⁻¹U⁻¹R² = (e₂ e₃ e₄)
对于旋转来说,以上的分析,最少只能的道 两个 角块(或 棱块)的旋转,我们无法做到 仅仅旋转 一个角块(或 棱块)。
上面,给定的公式都保证 角块(或 棱块)的旋转 时,所有小块位置不变,但 实际上,不一定需要这么严格,我们可以允许 与旋转小块同处一个面 内 小块的位置变换。通过暴力搜索,我们得到了公式B:
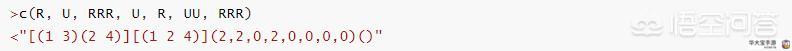
即,
RUR⁻¹URU²R⁻¹ = (c₁ c₃)(c₂ c₄)(e₁ e₂ e₄)(v₂, v₂, v₀, v₂, v₀, v₀, v₀, v₀);
以及,公式A:

即,
FRUR⁻¹U⁻¹F⁻¹ = (c₁ c₂)(c₃ c₄)(e₁ e₂ e₃)(v₀, v₂, v₁, v₀, v₀, v₀, v₀, v₀)(w₀, w₁, w₁, w₀, w₀, w₀, w₀, w₀, w₀, w₀, w₀, w₀);
公式 AB 都是 只 改变 顶层 位置的 操作。
其实,公式A就是 F[R, U]F⁻¹,其中 [R, U]:

[R, U] 的功效是 (e₁ e₂ e₇) ,即,将 顶层棱块 e₁ e₂ 和 中层 棱块 e₇ 轮换,但副作用 (c₂ c₇) 变动了 底层。不过幸运的是,我们找到了 [F⁻¹, U⁻¹]:

[ F⁻¹, U⁻¹] 的功效 和 [R, U] 类似,而其副作也是 (c₂ c₇)。因为 (c₂ c₇)(c₂ c₇) = 1,所以 [U⁻¹, F⁻¹] 的 刚好可以抵消 [R, U] 的副作用。于是,我们就得到了 公式A的附带公式:
[R, U] [ F⁻¹, U⁻¹] 和 [ F⁻¹, U⁻¹] [R, U]
功效分别是 (e₁ e₂ e₇ e₄ e₃) 和 (e₁ e₂ e₃ e₄ e₇),即,将顶层的 四个棱块 与 中层 的 棱块 e₇ 轮转。
在魔方数学原理的指导下,通过这种计算机暴力搜索的方式,我们还可以找到很多有用的公式,目前紧紧OLL公式就有 57 个,而更多的复杂公式几百上千。
众所周知的 ”七步公式还原法“(层先法) 就包括了从这些公式中选出来的 一组基础公式(包括上面提到的 公式ABCD)。(七步公式还原法,已经有条友在回答中详细介绍过了,我这里就不累述了。)
不知不觉,已经写了 5千余字了。关于魔法群还有很多更深入的内容,例如:上帝数 等,由于篇幅有限,这里不能一一展开,以后有机会再说。
(小石头,数学水平有限,出错在所难免,希望各位老师和同学批评指正。)
(补充 2019/10/30)
我将辅助工具的代码放在这里,以便想要自己试验的条友复制粘贴。
运行环境:chrome 浏览器;
文件名:rc.html,包含代码:
<script>
const s0 = [[1, 2, 3, 4, 5, 6, 7, 8],
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]];
const U = [[[1, 2, 3, 4]],[[1, 4, 3, 2]], [0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]];
const D = [[[5, 8, 7, 6]],[[9, 10, 11, 12]],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]];
const F = [[[1, 6, 7, 2]],[[3, 8, 11, 7]], [1, 2, 0, 0, 0, 2, 1, 0],[0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0]];
const B = [[[3, 8, 5, 4]],[[1, 6, 9, 5]], [0, 0, 1, 2, 1, 0, 0, 2],[1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0]];
const L = [[[1, 4, 5, 6]],[[4, 5, 12, 8]], [2, 0, 0, 1, 2, 1, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]];
const R = [[[2, 7, 8, 3]],[[2, 7, 10, 6]], [0, 1, 2, 0, 0, 0, 2, 1],[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]];
function perform(state, ... operations) {
for(var g of operations) {
var newstate = [g[0].reduce((l, c) => permute(l, c), state[0]),
g[1].reduce((l, c) => permute(l, c), state[1])];
newstate[2] = turn(state[0], state[2], newstate[0], g[2], 3);
newstate[3] = turn(state[1], state[3], newstate[1], g[3], 2);
state = newstate;
}
return state;
}
function permute(location, cycle) {
var newlocation = Array.from(location);
for(var i = 0; i < cycle.length - 1; i++) {
newlocation[cycle[i] - 1] = newlocation[cycle[i+1] - 1];
}
newlocation[cycle[cycle.length - 1] - 1] = location[cycle[0] - 1];
return newlocation ;
}
function turn(oldlocation, oldorientation, newlocation, spin, mod) {
var neworientation = [];
for (var i = 0; i < newlocation.length; i++) {
var j = oldlocation.indexOf(newlocation[i]);
neworientation[i] = (oldorientation[j] + spin[i]) % mod;
}
return neworientation;
}
function parse(state) {
return [parse_cycle(state[0]), parse_cycle(state[1]),
Array.from(state[2]), Array.from(state[3])
];
}
function parse_cycle(location) {
var flags = [], cycles = [];
for (var i = 0; i < location.length; i ++) {
if (i + 1 != location[i] && !flags[i]) {
var cycle = [i + 1, location[i]], j = location[i] - 1;
while(true) {
flags[j] = 1;
if (location[j] == i + 1)
break;
cycle.push(location[j]);
j = location[j] - 1;
}
cycles.push(cycle);
}
}
return cycles;
}
function compose(... operations) {
return parse(perform(s0, ... operations));
}
const str = arr => arr.reduce((s, x) => s +
(x[0] instanceof Array ? '[(' + x.map(y => y.join(' ')).join(')(') + ')]' :
(x.length == 0 ? '[]' : '(' + x.join() + ')')), '')
.replace('(0,0,0,0,0,0,0,0)', '()')
.replace('(0,0,0,0,0,0,0,0,0,0,0,0)', '()');
const c = (... ops) => str(compose(... ops));
const UU = compose(U, U), UUU = compose(U, U, U);
const DD = compose(D, D), DDD = compose(D, D, D);
const FF = compose(F, F), FFF = compose(F, F, F);
const BB = compose(B, B), BBB = compose(B, B, B);
const LL = compose(L, L), LLL = compose(L, L, L);
const RR = compose(R, R), RRR = compose(R, R, R);
const cycle = (... x) => [[x], [], s0[2], s0[3]];
const M = [[],[[2,4,12,10]],[0, 0, 0, 0, 0, 0, 0, 0], [0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1]];
const MMM = compose(M, M, M);
function perm(arr, callback, index){
var swap = (a, i, j, t) => (t = a[i], a[i] = a[j], a[j] = t);
index = index || 0;
if (index < arr.length) {
for (var j = index; j < arr.length; j++) {
swap(arr, index, j);
if (perm(arr, callback, index + 1)) return true;
swap(arr, index, j);
}
}
else {
return callback(arr);
}
}
</script>
文件名:rc2.html,包含代码:
<script>function perm(arr, callback, index){ var swap = (a, i, j, t) => (t = a[i], a[i] = a[j], a[j] = t); index = index || 0; if (index < arr.length) { for (var j = index; j < arr.length; j++) { swap(arr, index, j); if (perm(arr, callback, index + 1)) return true; swap(arr, index, j); } } else { return callback(arr); }}R._tag = "R"; RRR._tag = "R⁻¹"; U._tag = "U", UUU._tag = "U⁻¹";perm([RRR, UUU, R, U, RRR, UUU, R, U, R, UUU], x => { var g = compose(... x); console.log("+"); if (g[0].length == 0 && g[1].length == 1 && g[1][0].length == 3 && g[2].toString() == s0[2].toString() && g[3].toString() == s0[3].toString()) { console.log(x.reduce((y, z) => y + z._tag, "")); return true; }});</script>
三,魔方背后的数学原理
魔方被称为“智力游戏界的三大不可思议”之一,是由匈牙利布达佩斯建筑学院的厄尔诺·鲁比克发明的。他所发明的就是最常见的三阶魔方,由6个中心块,12个棱块,8个角块组成。最初,鲁比克教授发明魔方就是作为教具让他的学生去理解空间结构的。谁知,这一发明却很快风靡全球。


自从鲁比克教授开始在全世界推广魔方之后,各种各样的魔方不断被发明出来。现在的正阶魔方已经可以做出33阶魔方了,中国量产的最高阶魔方是17阶魔方。而且,现在质量最好和速拧最好的魔方都是中国制造的。随着魔方做的越来越好,复原魔方的时间也在不断的被刷新。现在,最快复原三阶魔方也仅仅只需要三四秒钟,比赛的魔方种类也越来越多。

就算没有玩过魔方的人也知道,魔方的复原是有公式的。而这些公式则是由数字和字母组成的,转动不同的面或不同的层都有对应的字母,学会认识这些字母才能更好的学会复原魔方。
复原三阶魔方最基础的方法是层先法,也就是一层一层的做。现在层先法最常见的步骤是需要七大步就可以还原整个魔方,而且基础的方法也不需要记很多公式。只要用心去学习,还是比较容易学会三阶魔方的。




 当然,学会复原魔方只是最基础的操作。要想提升速度,还得经过大量的练习和学习高级的方法CFOP,这个方法不仅需要记忆的公式很多,还需要你自己对魔方有一定的见解,这样才能练得更好。
当然,学会复原魔方只是最基础的操作。要想提升速度,还得经过大量的练习和学习高级的方法CFOP,这个方法不仅需要记忆的公式很多,还需要你自己对魔方有一定的见解,这样才能练得更好。

路过的小伙伴们,你们会哪些魔方呢?

四,魔方有几种
生活中,我们或多或少都接触过魔方。魔方(Rubik’s Cube),最早被称为“魔术方块”,与中国人发明的“华容道”、法国人发明的“独立钻石”一起被称为智力游戏界的三大不可思议。魔方,英文名为Rubik's Cube,又叫鲁比克方块,最早是由匈牙利布达佩斯建筑学院厄尔诺·鲁比克(又称作厄尔诺·卢比克)教授于1974年发明的。魔方竞速是一项手部极限运动。因为足够多变,复杂烧脑,能独立还原之人少之又少。因此,在很多人眼里“会玩魔方”= 高智商。
当时是为了帮助学生更好地认识空间立体几何。后来他在魔方的6个面涂上不同颜色,转动数步之后,魔方被打乱,但想要复原至初始状态是有一定难度的。有商人敏锐地嗅到其中的商机,成功地将魔方作为一种益智玩具推向全世界,与华容道、独立钻石并称世界三大智力游戏。

别看个头小,魔方可拥有43,252,003,274,489,856,000 种变化!来试试看你能答对几条关于魔方的冷知识吧!
1.三阶魔方一共有多少块?
“这太好算了,3x3x3=27块!”
魔方的构成 三阶魔方是由 3×3×3-1=26 个小方块组成的立方体,有 6 个面(还原之后每个面颜色相同,共 6 种颜色),每个面有 9 个 小面,共 54 个小面。26 个小方块包括 6 个中心块(仅一个可见 面)、12 个棱块(两个可见面)、 8 个角块(三个可见面)
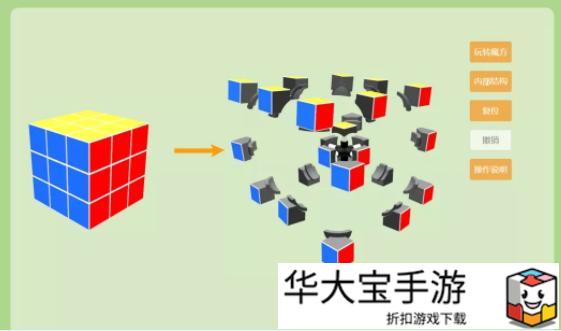 没错,最早由鲁比克教授设计的魔方是由27块组成的。但是如今的魔方将最中央的方块“变成”让魔方转动更顺滑的中心轴,所以现在的三阶魔方一共有26块,你答对了么?
没错,最早由鲁比克教授设计的魔方是由27块组成的。但是如今的魔方将最中央的方块“变成”让魔方转动更顺滑的中心轴,所以现在的三阶魔方一共有26块,你答对了么?
2.世界上复原魔方时间最久的是多少?
“肯思考的话,估计也就一两个月吧”
No No No,英国《每日邮报》报道,英格兰汉普郡的建筑工人帕克从1983年买下魔方开始,一直在为复原魔方努力,历经26年、2.7万个小时后终于成功。他也成为了世界上解开魔方用时最长的人(这样的世界纪录笔者可不想要)
3.最高阶的魔方有多大?
“五阶?不能比七阶多了吧....”
目前可以批量生产的最高阶魔方已经达到了17阶,有些爱好者甚至自己用3D打印机制作了33阶魔方哦~(这转起来可真是个体力活....)
4.什么样的人魔方玩的快?
“成年人?天才吧……”
这就更是大错特错啦,包揽多项世界魔方赛冠军的“菲神”是“90后”,很多“00后”、“10后”更是成绩超过成年人,并且玩起了“异型魔方”,这都和他们日常的勤奋练习分不开。听说“菲神”备赛的时候一天要练习十个小时,果然是台上四秒钟,台下十年功啊。

有限中蕴含着无限:魔方是有限块体单元的有序组合,可以有无限的变化。
无限中蕴含着有限:无限万化的魔方组合中蕴含有限的规律与本质核心。
魔方具有深刻的哲学寓意,既有隐性的内在规则与核心本质,又有显性的形式变化。用魔方类比学习生活,形象的阐释生产生活中蕴含的道理,便于理解和应用。
拆解魔方的过程,就是一个逐渐精简知识/问题现象的过程,逐渐接近知识/现象/问题的本质核心。拆解魔方的过程形象的解释了“为道日损”的含义,最后整体的魔方变形离散单元的时候,恰好解释了“道在其中,而不见其形”的含义。
组装魔方的过程就是从认知原点/知识原点逐渐增加知识/现象/问题复杂性的过程,使问题更加完善。组装魔方的过程形象的解释了“为学日益”的含义,最后离散单元有序组合成整体的过程,充分体现了“现象是离散单元有序组合”的含义。
转动魔方的过程,就是一个分析问题、理解问题,解决问题的过程,感知-观察-测量-分析-试验-内化-理解-判断-选择-实践-评价-内省的过程。经过刻意学习和练习,就会形成完整的思考回路,形成清晰的思路和操作方法,经过刻意的练习,使魔方从有序到无序,从无序到有序,完成从生手-新手-熟手-高手的转变。如果不去认真思考,专心学习,刻意练习,实践反思,就会处于混沌状态中而不能自拔。

魔方有很多种类,三阶是最基础的一种,其他种类的魔方很多都是三阶的变形,比如二阶、四阶、棕子魔方等,通过类比三阶魔方,可以举一反三,将其他魔方降阶为三阶,还原其主体部分,剩下的部分只需要解决当前这种魔方的某些特殊情况即可。
魔方有一套完整、简洁、准确、美妙的表达系统。利用前(Front)、后(Back)、左(Left)、右(Right)、顶(Up)、底(Down)这六个面(side)的英文单词首字母大写来表示某个面的转动。同时,每个面的旋转又有两种方向:顺时针和逆时针,在右上角标记',则为逆时针旋转90度,若没有标记,则为顺时针旋转90度。所以,R U R'的含义是:首先将右面顺时针旋转90度,再将顶面顺时针旋转90度,最后将右面逆时针旋转90度。此外还有更多转动的符号表达,如双层、中层、整体转动等,本文只是简介,不再赘述。
层先法:魔方有三层,层先法则是一层一层地还原,也是魔方最流行的初级复原方法,有些朋友“复原”第一面的方法,其实层先法的前几步比较相似。掌握基础的层先法后可以通过学习更多case的公式,升级为CFOP法,这也是目前速拧项目应用最广泛的复原方法。
桥式:这种解法先搭建两个1×2×3的块(也就是“桥”),然后再复原剩下的4个角、6个棱及4个中心块。其主要特点有:灵活,公式量少,步数少,但由于需借助更强的观察能力和预判能力,且相对来说不易理解,不太适合初学者直接上手。也正是因为其搭桥的方式很灵活,掌握之后或许能展现出比CFOP更加强大的威力。
角先法,棱先法:顾名思义,先复原角块或棱块,在某种意义上,盲拧采用的就是这类方法。
玩魔方必知的心理学理论心理学家维纳说:成败=能力+努力+难易+运气+(身心+环境),而这六种因素分别有什么特点,我来画张示意图:


1.魔方中的排列组合
由排列组合中的乘法和加法原理可知,三阶魔方共有 8!×38×12!×212 3×2×2 种状态。除去被轴固定的 6 个中心块外,剩 余 20 个小块, 8 个角块放在 8 个角位置,全排列为 8!,每个 角块的三种颜色因为方向的不同又有 3 种方法,因此共有 8!× 38 种排列;同理,12 个棱块共有 12!×212 种排列。

但是魔方还原 过程中,保持其他小块不动时,不可以单独改变一个角块的朝 向,不可以单独改变一个棱块的朝向,也不可以单独交换一对 棱块或一对角块的位置,因此需要除去 3×2×2。由此可见,要凭 运气把一个颜色斑驳的魔方还原成同面同色几乎是不可能的。

2.魔方的对称性
对称是一个几何图形 Φ 的如下性质:在某个变换群 G 的 作用下, Φ 被映射到自身上,这个群称为对称群。如果变换群 G 是一条直线,那么几何图形 Φ 就是关于直线 G 的对称图形;如 果变换群 G 是一个点,那么几何图形 Φ 就是以点 G 为中心的 对称图形。
若以点 G 为中心的对称图形 Φ 在平面内绕着 G 旋 转 360°/n(n 是一个整数)后与自身重合,那么 Φ 有一个 n 阶对 称,且 G 称为其对称中心。如图 a, b, c 分别是以 O 为中心的 2 阶、 4 阶、 3 阶对称。这样的对称性在正方体中完全展现,只是此 时绕平面内某点的旋转换成了空间中绕某直线的旋转。
三阶正方体魔方具有 2 阶、 3 阶、 4 阶对称轴,这样的对称 性是除了球体以外的其他物体所不能比拟的。魔方的还原过 程就在于旋转中魔方色块位置的交换,对于魔方每层每次的旋 转都是绕着该层中心块的变换,这样的保持点间距离不变的空.
3.魔方群
魔方的转动是指将魔方某个面上的所有块顺时针(面对该面)旋转 90°。相应的,若是逆时针旋转则称为逆转动。为了记录下转乱、复原的过程,习惯上采用由 David Singmaster 发明的符号来书写。以英文 Up(上)、Down(下)、Front (前)、Back(后)、Left(左)、Right(右)的第一个字母分别表示魔 方的上、下、前、后、左、右六个面的转动;用小写字母 u、 d、 f、 b、 l、 r 表示各面及相应的中心块;用 xy 来表示位于 x 面 y 位置的 棱块小面,如 uf 表示 u(上)面 f(前)位置的小面;用 xyz 表示位 于 x 面 yz 位置的角块小面,如 ufr 表示位于示 u(上)面 fr(前 右)位置的小面。
在对魔方任意一个面进行转动的时候,该面所在层的中心 块不会改变,其余 20 个小面的位置随之发生改变,这样的转动 可以用一系列小面的置换来表示:U=(ulb ubr urf ufl )(ub ur uf ul)(bul rub fur luf)(bu ru fu lu)(bru rfu flu lbu) D=(dbl dlf dfr drb)(db dl df dr)(bld lfd frd rbd)(bd ld fd rd)(bdr ldb fdl rdf) F=(flu fur frd fdl)(fu fr fd fl)(ufl rfu dfr lfd)(uf rf df lf )(urf rdf dlf luf) B=(bul bld bdr bru)(bu bl bd br)(ulb ldb drb rub)(ub lb db rb)(ubr lbu dbl rbd) L=(luf lfd ldb lbu)(lu lf ld lb)(ufl fdl dbl bul)(ul fl dl bl)(ulb flu dlf bld) R=(rfu rub rbd rdf)(ru rb rd rf)(urf bru drb frd)(ur br dr fr)(ubr bdr dfr fur)

设 G= U, D, F, B, L, R 是魔方所有转动生成的集合,可以 证明该集合以合成作为运算构成一个群,称为魔方群。它是上 述一系列小面的置换作为生成元的一个循环群。G 中的元素代表了所有置换的情形,魔方变换的所有状态 都能够找到与之相应的元素,魔方从还原状态经过一系列变化 再次还原,实现了一次循环,实际也是 G 中的元素经过周期性 的操作能够实现的,从中可以看到魔方还原与循环群的共性。

当初厄尔诺·鲁比克教授发明魔方,就是将其作为帮助学生增强空间思维能力的教学工具。经过观察、分析,我们不仅可 以找到魔方中蕴涵的数学知识,也看到了魔方中的教学因素:通过魔方的外观展示和结构剖析帮助学生建立立体模型的概 念,增强空间观念,通过魔方还原有助于学生深刻感受置换、循环,理解群论的相关概念,从外观一个简单的立体图形,到还原 过程中的各类变换 有助于学生逻辑思维能力的学习和提升。
五,魔方的方法
针对每一个问答都本着绝不大胆胡说,只管小心求证的态度,疯评科技来解答您的提问。
魔方的原理主要是依托于正方体的六个面的中心块而进行转动变化的,这6个中心就是
永远在固定位置,这也是还原魔方的最核心依据。因此需要考虑的如何去转动还原其它8个角块,12个棱块,最终沿着这些思路而想出各种不同的解法。
在6个中心块定好朝向后,正好构成了一个坐标系,8个角色块全排列8!,而每个角色块有3种朝向,所以是8!*(3的8次方),12个棱色块全排列每个有2种朝向是12!*(2的12次方),这样相乘是一个总的变化数量,但有很多重复的情况。对于8个角块,7个角块朝向定好了,第8个角块朝向就定了,所以8个角块的朝向实际上只有3的7次方种可能性,12个棱块也类似,11个棱块的朝向确定了,第12个也就确定了,所以12个棱块的朝向只有2的11次方种可能性,另外呢,就是在角块和棱块的全排列8!*12!里(角块只能和角块交换,棱块只能和棱块交换,所以不是20!),有一半的可能性是不被允许的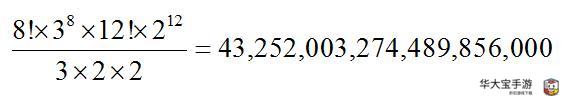
这么多种变化。
魔方按照形状可分为正阶和异性魔方两种。
正阶魔方
所谓正阶魔方就是指的2阶,3阶,4阶这样下去,目前量产的最高阶魔方是17阶,以后可能会能量产出来更高阶的魔方。
异性魔方
不规则的魔方就叫做异形魔方,各种各样,也比较有意思,有几十种之多。

我们在电视上可以看到会玩的人还原的非常快,只有几秒钟,这都是高级还原方法,对于新手刚入门,可以通过入门方法还原,几天即可自学会,刚学会,五六分钟完全可以复原。
初级还原方法——层先法
层先法,顾名思义就是一层一层的进行还原。
①对好白色底面十字
②复原白色底面+侧面T字
③复原中间层
④对好黄色顶面十字
⑤复原顶层黄色面
⑥复原顶层角块
⑦复原最后几个棱块
这个没什么特别的方法,就是熟能生巧了,当然有一点点空间想象力会好一点。
高级还原方法——CFOP
高级还原方法就主要是记公式了,大概119个公式,有的公式非常长,通过配合魔方手法的肌肉记忆,并不难。
①对好底层十字
②复原前两层
③对好顶层朝向
④对好顶层顺序
魔方比赛主要分为速拧和盲拧两种。
这个很好理解,速拧就是在随机打乱公式打乱下比拼复原速度,分单次成绩和平均成绩。
盲拧就是盲眼比赛,可以有15秒的观察时间,计入成绩时间内。
魔方的原理就是通过固定一些中心块或者固定几对中心块的相对位置,再进行复原的方式,或通过总结经验,或通过计算机计算出最优解,形成固定公式来解。
总结:以上内容就是宝宝游戏提供的魔方的原理是什么?(魔方的原理是什么,有什么技巧解开魔方)详细介绍,大家可以参考一下。









